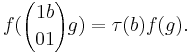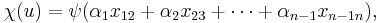Whittaker model
In representation theory, a branch of mathematics, the Whittaker model is a realization of a representation of a reductive algebraic group such as GL2 over a finite or local or global field on a space of functions on the group. It is named after E. T. Whittaker even though he never worked in this area, because (Jacquet 1966, 1967) pointed out that for the group SL2(R) some of the functions involved in the representation are Whittaker functions.
Irreducible representations without a Whittaker model are sometimes called "degenerate", and those with a Whittaker model are sometimes called "generic". The representation θ10 of the symplectic group Sp4 is the simplest example of a degenerate representation.
Contents |
Whittaker models for GL2
If G is the algebraic group GL2 and F is a local field, and τ is a fixed non-trivial character of the additive group of F and π is an irreducible representation of G(F), then the Whittaker model for π is a representation π on a space of functions f on G(F) satisfying
Jacquet & Langlands (1970) used Whittaker models to assign L-functions to admissible representations of GL2.
Whittaker models for GLn
Let  be the general linear group
be the general linear group 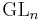 ,
,  a smooth complex valued non-trivial additive character of
a smooth complex valued non-trivial additive character of  and
and  the subgroup of
the subgroup of 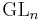 consisting of unipotent upper triangular matrices. A non-degenerate character on
consisting of unipotent upper triangular matrices. A non-degenerate character on  is of the form
is of the form
for 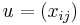 ∈
∈  and non-zero
and non-zero 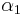 , ...,
, ..., 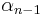 ∈
∈  . If
. If  is a smooth representation of
is a smooth representation of 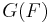 , a Whittaker functional
, a Whittaker functional  is a continuous linear functional on
is a continuous linear functional on  such that
such that  for all
for all  ∈
∈  ,
,  ∈
∈  . Multiplicity one states that, for
. Multiplicity one states that, for  unitary irreducible, the space of Whittaker functionals has dimension at most equal to one.
unitary irreducible, the space of Whittaker functionals has dimension at most equal to one.
Whittaker models for reductive groups
If G is a split reductive group and U is the unipotent radical of a Borel subgroup B, then a Whittaker model for a representation is an embedding of it into the induced (Gelfand–Graev) representation IndG
U(χ), where χ is a non-degenerate character of U.
See also
- Gelfand–Graev representation, roughly the sum of Whittaker models over a finite field.
- Kirillov model
References
- Jacquet, Hervé (1966), "Une interprétation géométrique et une généralisation P-adique des fonctions de Whittaker en théorie des groupes semi-simples", Comptes Rendus Hebdomadaires des Séances de l'Académie des Sciences. Séries A et B 262: A943--A945, ISSN 0151-0509, MR0200390
- Jacquet, Hervé (1967), "Fonctions de Whittaker associées aux groupes de Chevalley", Bulletin de la Société Mathématique de France 95: 243–309, ISSN 0037-9484, MR0271275, http://www.numdam.org/item?id=BSMF_1967__95__243_0
- Jacquet, H.; Langlands, Robert P. (1970), Automorphic forms on GL(2), Lecture Notes in Mathematics, Vol. 114, 114, Berlin, New York: Springer-Verlag, doi:10.1007/BFb0058988, MR0401654, http://www.sunsite.ubc.ca/DigitalMathArchive/Langlands/JL.html#book
- J. A. Shalika, The multiplicity one theorem for
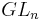 , The Annals of Mathematics, 2nd. Ser., Vol. 100, No. 2 (1974), 171-193.
, The Annals of Mathematics, 2nd. Ser., Vol. 100, No. 2 (1974), 171-193.